Uji Kecekungan (Turunan Kedua)

Turunan kedua mengukur percepatan momentum.
Jika turunan pertama menunjukkan kecepatan perubahan harga, maka turunan kedua menunjukkan apakah perubahan itu semakin cepat atau melambat.

🔹 Flowchart Logika Kecekungan

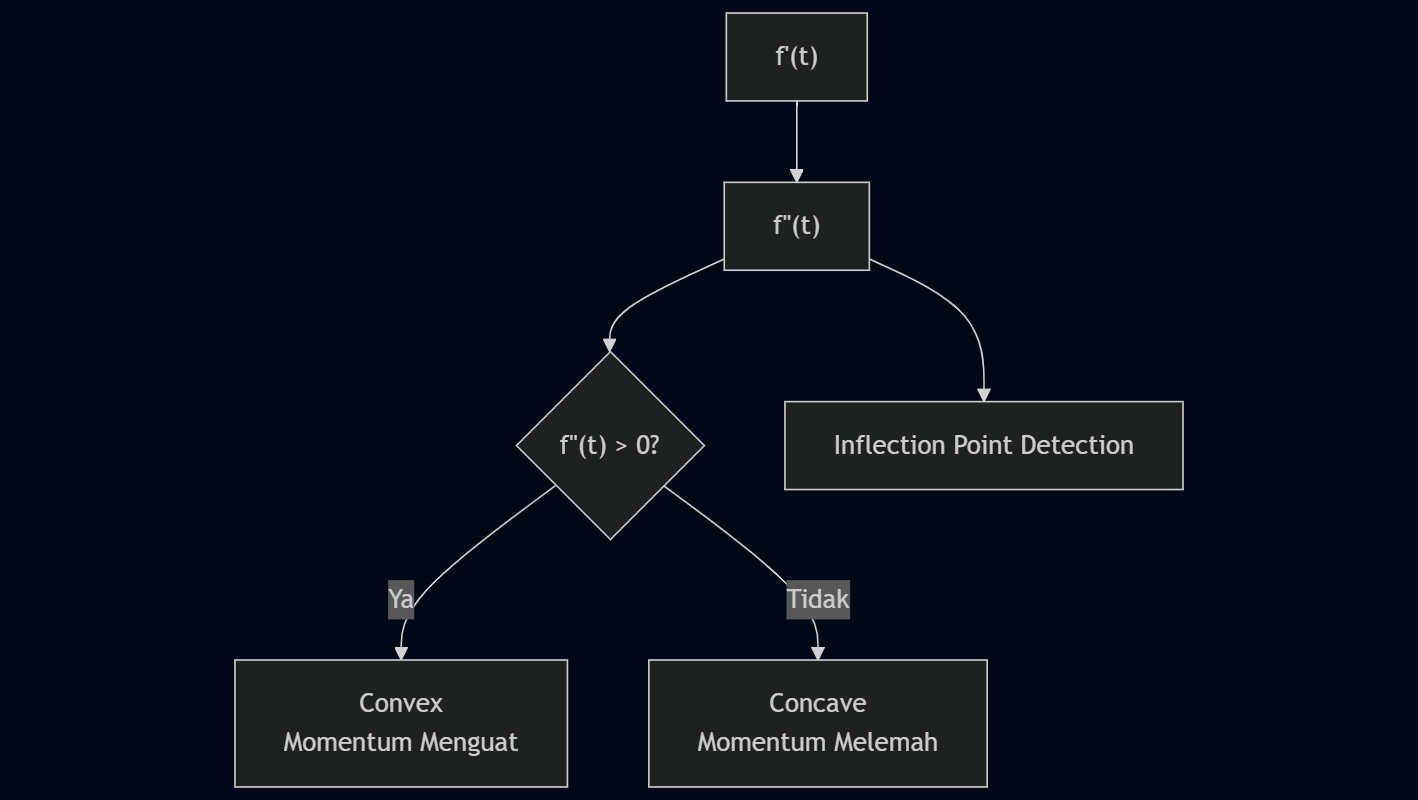
1. Definisi Turunan Kedua

Dalam bentuk diskrit yang digunakan dalam proyek:

2. Interpretasi Tanda Turunan Kedua

Arti tanda:

• $f''(t) > 0$ → convex (momentum menguat)
• $f''(t) < 0$ → concave (momentum melemah)

Interpretasi visual:

• Convex: grafik melengkung ke atas, tren mulai menguat
• Concave: grafik melengkung ke bawah, tren mulai melemah

3. Convexity Score

Convexity score menormalkan nilai turunan kedua agar lebih mudah dibaca:

Keterangan:

• $C \approx 1$ → convex sangat kuat (bullish momentum)
• $C \approx 0$ → concave sangat kuat (bearish momentum)

Parameter $k$ mengontrol sensitivitas.

4. Stability Index

Stability index mengukur konsistensi tanda turunan kedua.
Jika tanda turunan kedua sering berubah, tren dianggap tidak stabil.

Rumus:

5. Deteksi Titik Belok (Inflection Point)

Titik belok terjadi ketika turunan kedua berubah tanda:

Artinya:

• Kurva berubah dari convex → concave (potensi downtrend)
• Atau concave → convex (potensi uptrend)

Inflection point sering kali menjadi indikator awal reversal tren.

6. Contoh Singkat

Misalkan:

Karena:

Inflection point di t = 3 → reversal bullish.

7. Visualisasi Konsep

Alur Analisis Turunan

1. Hitung Turunan Pertama (f'(t))
   • Digunakan untuk mengukur momentum harga.
2. Hitung Turunan Kedua (f''(t))
   • Digunakan untuk membaca percepatan momentum.
3. Evaluasi Kecekungan (Convexity Check)
   • Jika convex:
     • Momentum Menguat
   • Jika tidak convex (concave):
     • Momentum Melemah
4. Deteksi Inflection Point
   • Perubahan tanda pada turunan kedua digunakan untuk mendeteksi titik belok (reversal).