Polynomial Regression (Smoothing)
Karena data harga kripto sangat berisik (noisy), menghitung turunan langsung dari harga mentah (raw price) akan menghasilkan:
- grafik velocity yang kacau,
- turunan kedua yang tidak stabil,
- sinyal palsu,
- inflection point yang tidak akurat.
🔹 Flowchart Proses Polynomial Smoothing
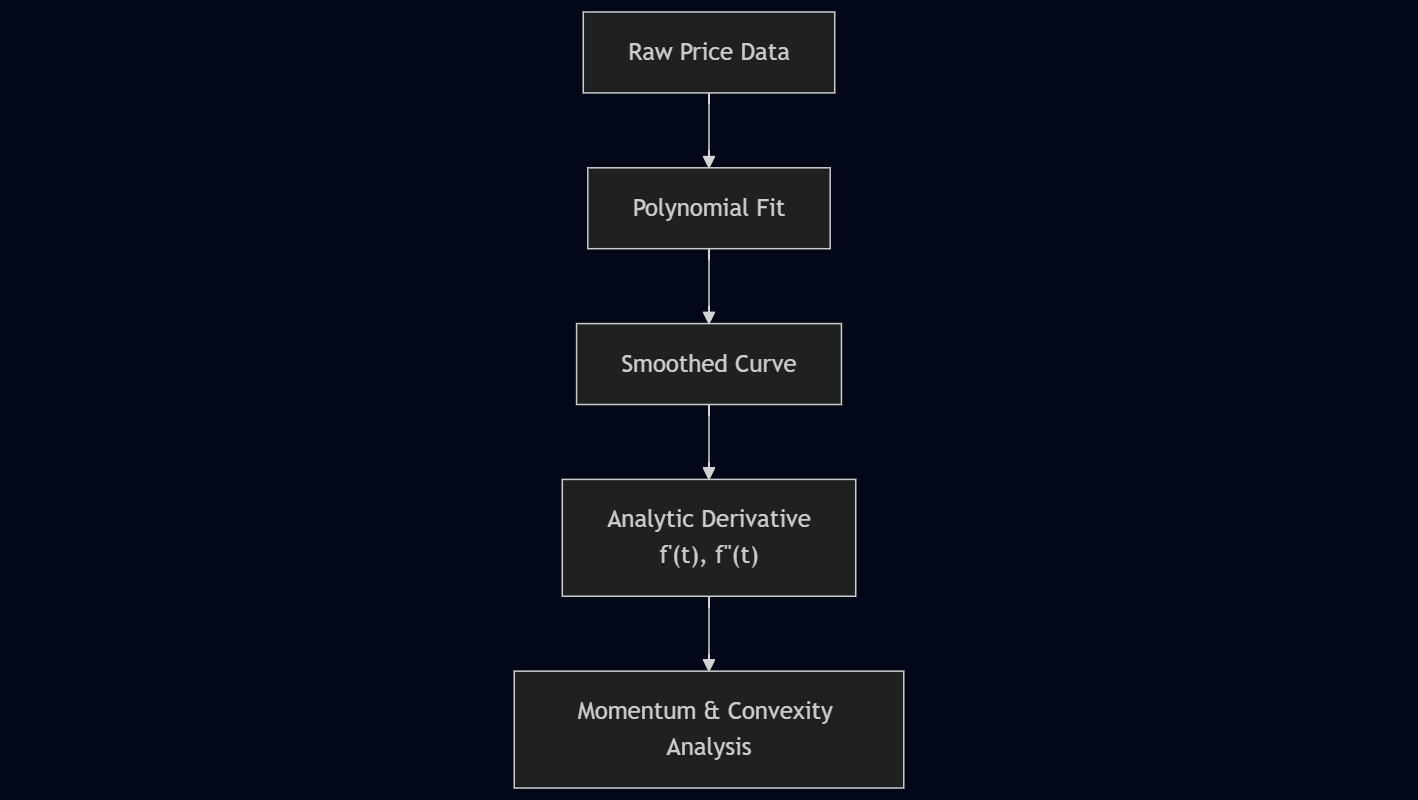
Oleh karena itu, digunakan polynomial regression untuk menghasilkan kurva harga yang halus (smoothed price).
1. Bentuk Umum Polinomial
2. Turunan Polinomial
Turunan pertama:
Keuntungan utama:
- dan dapat dihitung secara analitik ,
- hasilnya jauh lebih stabil dibanding metode finite difference langsung.
3. Mengapa Polynomial Regression Dipilih?
✔ Tidak membutuhkan parameter "window"
Berbeda dengan moving average.
✔ Tidak menyebabkan lag besar
Karena tidak melakukan rolling average.
✔ Turunan analitik → stabil dan halus
Sangat cocok untuk menghitung convexity dan inflection point.
✔ Lebih unggul dibanding smoothing sederhana
Seperti SMA, EMA, ataupun Gaussian filter.
4. Perhitungan dengan Least Squares
Regresi polinomial mencari koefisien:
5. Pemilihan Derajat Polinomial (Order)
| Derajat | Kelebihan | Kekurangan |
|---|---|---|
| 2–3 | Halus | Kurang fleksibel |
| 4–5 | Seimbang | Risiko overfit |
| 6+ | Fleksibel | Cenderung mengikuti noise |
6. Contoh Visualisasi Konseptual
Jika data harga: 64000 → 64012 → 63998 → 63990 → 64020
Raw price = bergerigi
Smoothed price = kurva mulus menggambarkan tren sesungguhnya
7. Manfaat Terhadap Perhitungan Turunan
Polynomial smoothing meningkatkan:
- akurasi velocity (turunan 1),
- stabilitas acceleration (turunan 2),
- kekuatan convexity score,
- deteksi inflection point.
Tanpa smoothing, nilai turunan akan terlalu liar untuk data kripto.
Ringkasan
| Komponen | Fungsi |
|---|---|
| Polynomial Regression | Menghaluskan grafik harga |
| Turunan Analitik | Stabil & akurat |
| Derajat Polinomial | Mengontrol fleksibilitas |
| Least Squares | Menghitung koefisien terbaik |